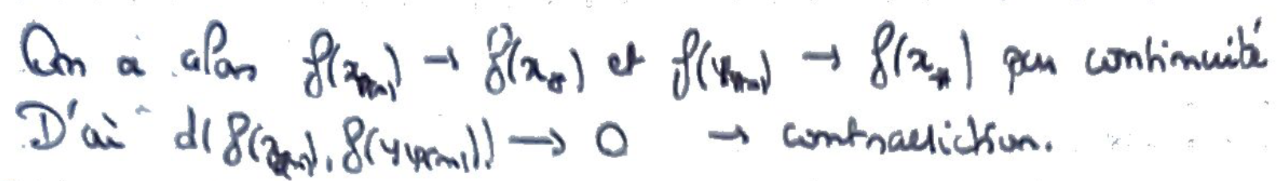On prend la caractérisation avec deux suites dont la distance tend vers \(0\) mais ^dont la distance entre les images ne tend pas vers \(0\) (on peut prendre arbitrairement grande quitte à extraire).

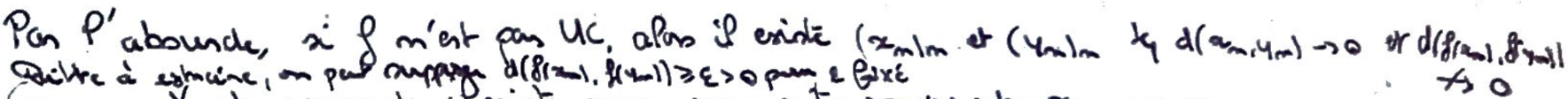
Par compacité, on a l'existence d'une sous-suite convergente pour les deux suites, qui convergent vers la même limite.

La continuité de \(f\) nous donne alors une contradiction.